Diese Seite funktioniert nur mit Javascript.
Die Einkommenselastizität2.4.2.2 Die direkte PreiselastizitätDie Kreuzpreiselastizität
ie direkte Preiselastizität der Nachfrage ist nichts anderes als die Elastizität der aggregierten Nachfragefunktion. Sie zeigt (näherungsweise) an, um wie viel Prozent die Nachfrage nach einem Gut sinkt, wenn der Preis um ein Prozent steigt. Sie ist bis auf den seltenen Ausnahmefall des Giffen-Gutes negativ, allerdings wird das in der Regel im ökonomischen Sprachgebrauch unterschlagen. Das verwirrt anfangs besonders dann, wenn von einer größeren oder steigenden Elastizität die Rede ist. Gemeint ist nämlich, dass der absolute Wert größer ist oder steigt. Der tatsächliche Wert einer größeren Elastizität ist kleiner.
Die Preiselastizität der Nachfrage wird mit dem Attribut "direkt" belegt, um sie von der Kreuzpreiselastizität zu unterscheiden. Da die Kreuzpreis- und Einkommenselastizität eine weit weniger wichtige Rolle spielen als die Preiselastizität, wird bei der Preiselastizität meist nur von der Elastizität gesprochen.
Wie sich später zeigen wird, kommt der direkten Preiselastizität der Nachfrage eine große Bedeutung zu. Von ihr hängt es z.B. ab, ob Preiserhöhungen zu Umsatzsteigerungen führen. Sie beeinflusst ganz wesentlich, wie stark Steuern auf das Produkt an die Konsumenten überwälzt werden können. Und sie bestimmt das Ausmaß, in dem marktbeherrschende Unternehmen die Konsumenten ausbeuten können (sog. Messung der Monopolmacht).
Mit Hilfe der Preiselastizität kann zwischen normalen Gütern und Giffen-Gütern unterschieden werden. Letztere besitzen eine positive Elastizität. Grundbedarfsgüter zeigen tendenziell eine geringere Preiselastizität als Luxusgüter, da bei steigenden Preisen die Einschränkung des Konsums von Grundbedarfsgütern schwerer fällt als der Verzicht auf Luxusgüter.
- Die Preiselastizität nimmt tendenziell mit dem Betrachtungszeitraum zu, da sich die Haushalte Preisänderungen mittel- bis langfristig besser anpassen können als kurzfristig. Ein vielleicht schon extremes, aber anschauliches Beispiel, bietet die Nachfrage nach Heizöl. Auf kurze Sicht stellen die Haushalte ihre Heizung nicht auf Gas um, wenn die Heizölpreise steigen. Ist jedoch auf Dauer mit hohen Heizölpreisen zu rechnen, wird die Alternative Gas für viele Bauherren und Modernisierer attraktiver.
- Je besser die Verfügbarkeit von Substituten ist, desto höher ist die direkte Preiselastizität der Nachfrage zu erwarten. Wenn zahlreiche und enge Substitute zur Verfügung stehen, können die Haushalte bei Preiserhöhungen leicht auf sie ausweichen. Ob Substitute zur Verfügung stehen und wie gut sie sind, kann mit der Kreuzpreiselastizität der Nachfrage gemessen werden. Das deutet auf einen Zusammenhang zwischen den Elastizitäten hin, der auch tatsächlich besteht, hier aber nicht weiter verfolgt wird.
- Wenn das betrachtete Gut einen hohen Anteil an den Ausgaben des Haushalts hat, spricht das für eine größere Nachfrageelastizität. Der Grund ist einfach, dass Preisänderungen für Güter mit einem geringen Ausgabenanteil für den Haushalt weniger spürbar sind.
Was will er damit zum Ausdruck bringen?
Werte der Preiselastizität nahe null deuten an, dass die Haushalte auf das Produkt angewiesen sind. Obwohl die Preise steigen, können sie nicht auf andere Produkte ausweichen oder ihren Konsum einschränken. Ein solches Problem haben z.B. Raucher. Trotz steigender Preise kommen sie nicht vom Tabak los. Nur wenigen gelingt es, z.B. auf Bonbons umzusteigen - ein entferntes Substitut fürs Rauchen - oder das Rauchen aufzugeben. Diese unelastische Nachfrage wird gelegentlich Suchtnachfrage genannt. Generell darf man einen dringlicheren Bedarf der Konsumenten bei Gütern mit geringerer direkter Preiselastizität der Nachfrage annehmen.
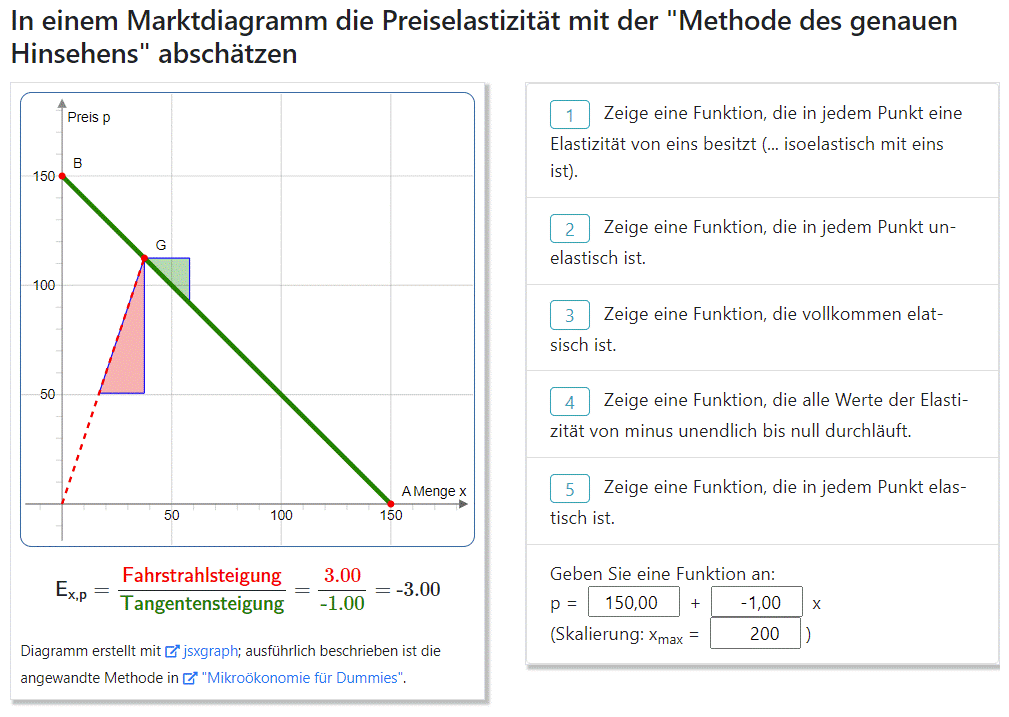
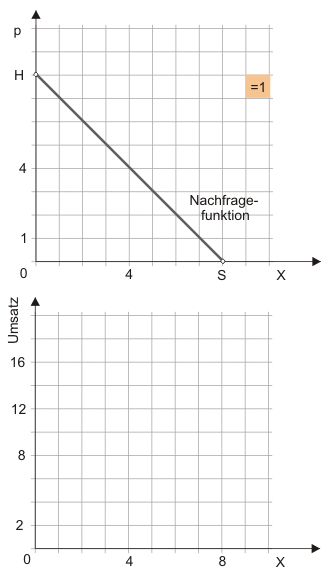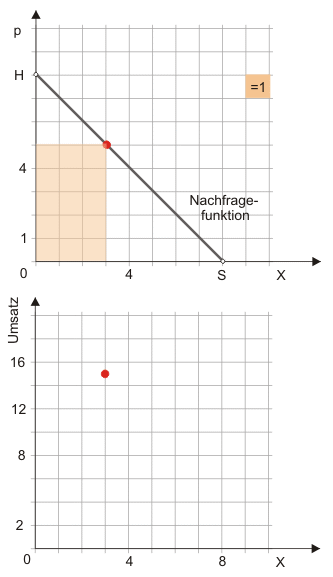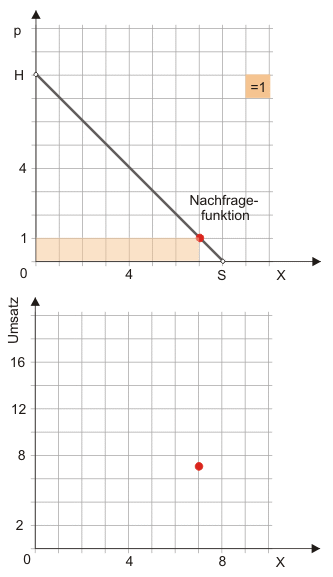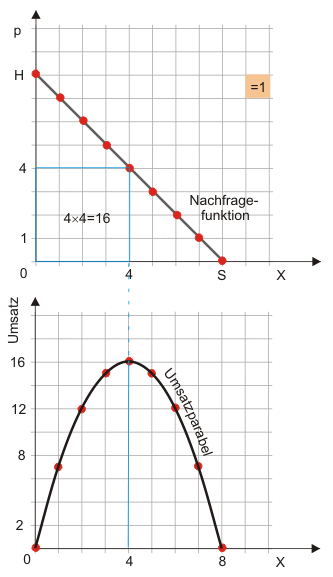
Achten Sie darauf, wie eine Fläche mit den Kantenlängen Preis und Menge im oberen Diagramm im unteren Diagramm als Skalar (Umsatz) an der Ordinate abgetragen wird.
Das Schlussbild zeigt, dass bei einer linearen Nachfragefunktion der Umsatz bei der halben Sättigungsmenge sein Maximum erreicht.
[Maussensitives Diagramm: Die Animation startet, wenn Sie das Diagramm anlklicken. Bitte etwas Geduld.]
Schritt für Schritt selbst steuern.
Für die direkte Preiselastizität der Nachfrage gilt, dass sie um den Wert eins über der Preiselastizität des Umsatzes liegt. Die Preiselastizität des Umsatzes ist also null, wenn die Preiselastizität der Nachfrage eins ist. Wenn aber die Preiselastizität des Umsatzes null ist, deutet das auf einen Extremwert des Umsatzes hin. In einer Grafik erkennt man das für den Spezialfall einer linearen Nachfragefunktion mit der 'Methode des scharfen Hinsehens':
Im oberen Diagramm zeigt die hinterlegte Fläche den Umsatz (= Preis mal Menge) an. Durch Abzählen der Kästchen lässt sich so der Umsatz bei alternativen Preisen bestimmen. Über die in beiden Diagrammen vorhandene Mengenachse wird der Umsatz im unteren Diagramm in 'Kästcheneinheiten' an der Ordinate abgetragen. Der Umsatz ist maximal, wenn der Preis dem halben Prohibitivpreis ($\frac{0H}{2}$) und die Menge der halben Sättigungsmenge ($\frac{0S}{2}$) entspricht. Das ist hier bei '16 Kästchen Umsatz' der Fall und farblich hervorgehoben.
Was die Grafik für eine lineare Funktion zeigt, lässt sich für den allgemeinen Fall wie folgt nachweisen:

Hannover (gum). Fahrgäste verloren und dennoch die Einnahmen verbessert - das ist die Bilanz der Üstra nach den ersten sechs Monaten dieses Jahres. Im ersten Halbjahr verlor der hannoversche Verkehrsbetrieb 2,1 Prozent Fahrgäste im Vergleich zum ersten Halbjahr 1996. 1,37 Millionen Kunden weniger stiegen in Busse und Bahnen - 65,45 Millionen Menschen transportierte die Üstra im ersten Halbjahr 1997 insgesamt.
Finanziell wirkte sich der Fahrgastverlust nicht negativ aus. Im Gegenteil: Wegen der seit Februar geltenden Tarifreform - Preisstufen und Tarifzonen wurden umgestellt, Fahrpreise um durchschnittlich sieben Prozent teurer - zahlten die Kunden im ersten Halbjahr 81,74 Millionen Mark in die Kassen der Üstra, fünf Millionen Mark mehr als zuvor. Diesen zusätzlichen Umsatz schreibt die Üstra auch der ,überproportionalen Anhebung der Tarife" bei verschiedenen Arten von Fahrkarten zu. ... (Quelle HAZ 16/17/8/97)
Direkte Preiselastizität der Nachfrage; vereinfachende Annahmen: einheitlicher Preis, ein Fahrgast = ein Ticket.
$$E = \cfrac{-2,1}{7} = -0,3 $$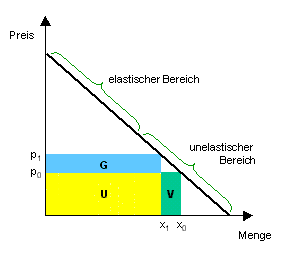
In der durch den Index 0 gekennzeichneten Ausgangssituation entspricht der Umsatz den Flächen U und V. Durch die Preiserhöhung wird aufgrund des Mengeneffektes die Fläche V an Umsatz verloren, aufgrund des Preiseffektes aber G hinzugewonnen.
Wenn also bekannt ist, dass die Nachfrageelastizität (dem Betrage nach) kleiner als 1 ist, kann sich die Gewinnsituation der Unternehmung mit der Preisanhebung nur verbessern. Erstens steigt der Umsatz und außerdem entsteht auch von der Kostenseite her ein positiver Effekt, wenn die Kosten mit sinkendem Fahrgastaufkommen zurückgehen.
Wie Gleichung (5) zeigt, steigt der Umsatz bei einer Preiserhöhung, wenn $E_{x,p}$ dem Betrage nach kleiner als 1 ist. Das Ergebnis ist also nicht nur im Fall der in der Grafik gezeigten linearen Nachfragefunktion gültig.
Die Elastizität des Umsatzes bzgl. des Preises kann man aus der unteren Grafik nicht ablesen, da hier nicht Umsatz und Preis, sondern Umsatz und Menge abgetragen sind. Durch Differenzieren des Umsatzes nach der Menge gewinnt man die sog. Amoroso-Robinson-Relation für den Grenzumsatz:
$$ \cfrac{\partial U}{\partial x} = \cfrac{dp}{dx}\cdot x + p \tag{6}$$ $$ \cfrac{\partial U}{\partial x} = \cfrac{p}{p} \Bigl( \cfrac{dp}{dx}\cdot x + p\Bigr) = p \Bigl(\cfrac{dp}{dx}\cdot \cfrac{x}{p} + 1\Bigr)\tag{7}$$ $$ \cfrac{\partial U}{\partial x} = p \Bigl( \cfrac{1}{E_{x,p}} + 1 \Bigr)\tag{8}$$- Skizzieren Sie eine vollkommen elastische Nachfragefunktion und zeichnen Sie für eine beliebige Menge den Umsatz ein.
- Erhöhen Sie die Menge um eine Einheit.
- Betrachten Sie die Umsatzentwicklung.
Wenn Sie diese drei Schritte durchführen, erkennen Sie, dass der Grenzumsatz unter dem Preis liegen muss, wenn die Nachfragefunktion nicht vollkommen elastisch ist (die Funktion eine negative Steigung zeigt).
Darüber lässt sich mit Hilfe der Amoroso-Robinson-Relation (8), auf die in der Monopoltheorie zurückzukommen sein wird, einiges aussagen:
Der Grenzumsatz liegt immer unter dem Preis.* Die direkte Preiselastizität der Nachfrage ist negativ. Damit ist der Klammerausdruck kleiner eins und der Grenzumsatz somit kleiner als der Preis $p$. Inhaltlich: Die nachgefragte Menge steigt nur an, wenn der Preis sinkt. Nur im Ausnahmefall einer vollkommen elastischen Nachfrage - waagerechte Nachfragefunktion - steigt der Umsatz mit einer weiteren Mengeneinheit genau um den Preis.
Der Grenzumsatz ist positiv im elastischen Bereich der Nachfrage. Hier führen ein sinkender Preis und eine steigende Menge zu höherem Umsatz. Der Klammerausdruck der Amoroso-Robinson-Relation liegt zwischen null und eins, da die Elastizität dem Betrage nach größer als eins ist. (Umgekehrt ist der Grenzumsatz negativ, wenn die Nachfrage unelastisch reagiert. Ein letztes Mal der Hinweis auf die Leserichtung im Marktdiagramm, in dem die obere Hälfte der Nachfragefunktion - im Unterschied zum verlinkten Diagramm mit umgekehrter Leserichtung - elastisch ).
Bei der halben Sättigungsmenge ist die Elastizität minus eins. Damit verschwinden Klammerausdruck und Grenzumsatz. Ein Grenzumsatz von null ist eine notwendige Bedingung für ein Umsatzmaximum.
Praxisbeispiel und Übung
Im nachstehenden Zeitungsartikel aus den Schaumburger Nachrichten v. 12.10.05, S. 4, finden Sie die Aussage "Finanziell ist uns eine durchschnittliche Ernte zu durchschnittlichem Preis lieber als eine reiche Ernte zu niedrigem Preis", sagt er.
Erklären Sie diese Aussage mithilfe des Begriffs "Elastizität" und stellen Sie den Zusammenhang im Marktdigramm dar.
Reich ist die Ernte, groß die Sorge
Konkurrenz aus Übersee und neue Vorschriften für Saisonarbeiter belasten Obstbauern im Alten Land
Von Rüdiger Meise
Jork. Mit leuchtenden Augen steht Apfelbauer Henning von Husen in seiner Plantage. "So viele und große Äpfel habe ich selten an den Bäumen gesehen", sagt er und dreht einen Apfel am Stiel vorsichtig vom Baum. Die Apfelpflücker im Alten Land sind derzeit täglich bis Einbruch der Dunkelheit auf den Beinen, das Wetter ist prächtig, die Ernte verspricht reich zu werden. Von Husen zeigt in die langen Reihen von Bäumen, die schwer an ihren glänzenden Früchten tragen, und sagt: "Ein solcher Anblick entschädigt für viel Mühe und Unsicherheit."
Unsicher ist der 41-Jährige vor allem, weil eine reiche Ernte längst kein Garant für großen Gewinn ist. Im Gegenteil. Wenn die Ernte in ganz Europa groß ausfällt, verfallen die Preise. Im vergangenen Jahr bekamen die Bauern etwa 20 Cent für das Kilo Äpfel, in diesem Jahr hofft von Husen auf 30 Cent. "Finanziell ist uns eine durchschnittliche Ernte zu durchschnittlichem Preis lieber als eine reiche Ernte zu niedrigem Preis", sagt er. [...] SN, 12.10.05, S.4.
LösungshinweisNach ähnlichen Seiten im WWW suchen